贝叶斯统计
后验概率(结果已知)
预先已知结果,然后根据结果估计(猜)原因的概率分布即 后验概率。 \(P(因\mid果) \\ \\ P(\theta\mid X)\)
先验概率(由历史求因)
不基于当前预测事件的结果,而是根据历史规律确定原因的概率分布即 先验概率 \(P(因) \\ \\ P(\theta)\)
似然估计(结果已知)
\[P(果\mid因) \\ \\ P(X\mid\theta)\]对于函数 $P(x\mid\theta)$,从不同的观测角度来看可以分为以下两种情况:
- 如果 $\theta$ 已知且保持不变, $x$ 是变量,则 $P(x\mid\theta)$ 称为概率函数,表示不同 $x$ 出现的概率。
- 如果 $x$ 已知且保持不变, $\theta$ 是变量,则$P(x\mid\theta)$ 称为似然函数,表示不同 $\theta$ 下, $x$ 出现的概率,也记作$L(\theta\mid x)$ 或$L(x;\theta)$ 或$f(x;\theta)$ 。
贝叶斯公式
\[P(\theta \mid X)=\frac{P(X \mid \theta) * P(\theta)}{P(X)}\] \[后验概率 =\frac{似然估计 * 先验概率}{evidence}\]$evidence$ 即为已发生的事实,是真实的证据,即为果。表示为: \(P(果)\)
频率学派与贝叶斯学派
频率学派与贝叶斯学派探讨不确定性这件事时的出发点与立足点不同。频率统计认为事件服从特定的分布,分布的参数虽然未知但是固定。如果进行大量独立重复实验,那么事件发生的概率一定会趋向事件的真实概率。比如抛硬币实验,如果重复无数次的话,出面证明的概率会非常接近0.5。频率学派从自然角度出发,试图直接为事件本身建模,即事件A在独立重复试验中发生的频率趋于极限 $p$,那么这个极限就是该事件的概率。
频率统计非常依赖实验次数,比如抛硬币实验中,只进行了1000次实验,而这1000次实验中600次是正面。如果根据频率统计的观点,那么正面出现的概率应该是0.6。但是事实上,如果硬币没有问题的话,正面出现的概率应该是0.5。所以说此时(实验次数少)的情况下,频率统计的结果并不合理。
而贝叶斯统计的思想是加入先验知识来对观察的现象做出推断。比如说,我们可以假设正面出现的概率位于 [0.4, 0.6] ( [0.4, 0.6]的区间假设就是先验知识)的区间内。然后基于这个假设,去估计正面出现的概率。贝叶斯学派并不从试图刻画事件本身,而从观察者角度出发。贝叶斯学派并不试图说事件本身是随机的,或者世界的本体带有某种随机性,这套理论根本不言说关于世界本体的东西,而只是从观察者知识不完备这一出发点开始,构造一套在贝叶斯概率论的框架下可以对不确定知识做出推断的方法。
频率学派的代表是最大似然估计;贝叶斯学派的代表是最大后验概率估计。
最大似然估计(MLE)/最大后验估计(MAP)/贝叶斯估计(BE)
给定一些数据样本 $x$,假定我们知道样本是从某一种分布中随机取出的,但我们不知道这个分布具体的参数 $\theta$。以抛硬币为例,假设我们有一枚硬币,现在要估计其正面朝上的概率$\theta$。为了对$\theta$进行估计,我们进行了10次实验(独立同分布,i.i.d.),这组实验记为$X=x_1,x_2,…,x_{10}$,其中正面朝上的次数为6次,反面朝上的次数为4次,结果为(1, 0, 1, 1, 0, 0, 0, 1, 1, 1)。
最大似然估计
最大似然估计(MLE,Maximum Likelihood estimation)可以估计模型的参数。最大似然估计的思想是使得观测数据(样本)发生概率最大的参数就是最好的参数,换句话说,其目标是找出最佳参数 $ \theta$,使得模型产生出观测数据 $x$ 的概率最大: \(\underset{\theta}{\operatorname{argmax}} P(X \mid \theta)\) 对一个独立同分布的样本集来说,总体的似然就是每个样本似然的乘积。针对抛硬币的问题,似然函数可写作: \(P(X\mid \theta)=L(X ; \theta)=\prod_{i=0}^n P\left(x_i \mid \theta\right)=\theta^6(1-\theta)^4\) 根据最大似然估计,使$L(X;θ)$取得最大值的 $ \theta$ 即为估计结果,令 \(\begin{aligned} L(X;θ)^{'}&= 6θ^5(1-θ)^4-4θ^6(1-θ)^3 \\ & = θ^5(1-θ)^3(6-10θ) \\ & =0 \end{aligned}\) 可得$\hat\theta =0.6$。似然函数图如下:
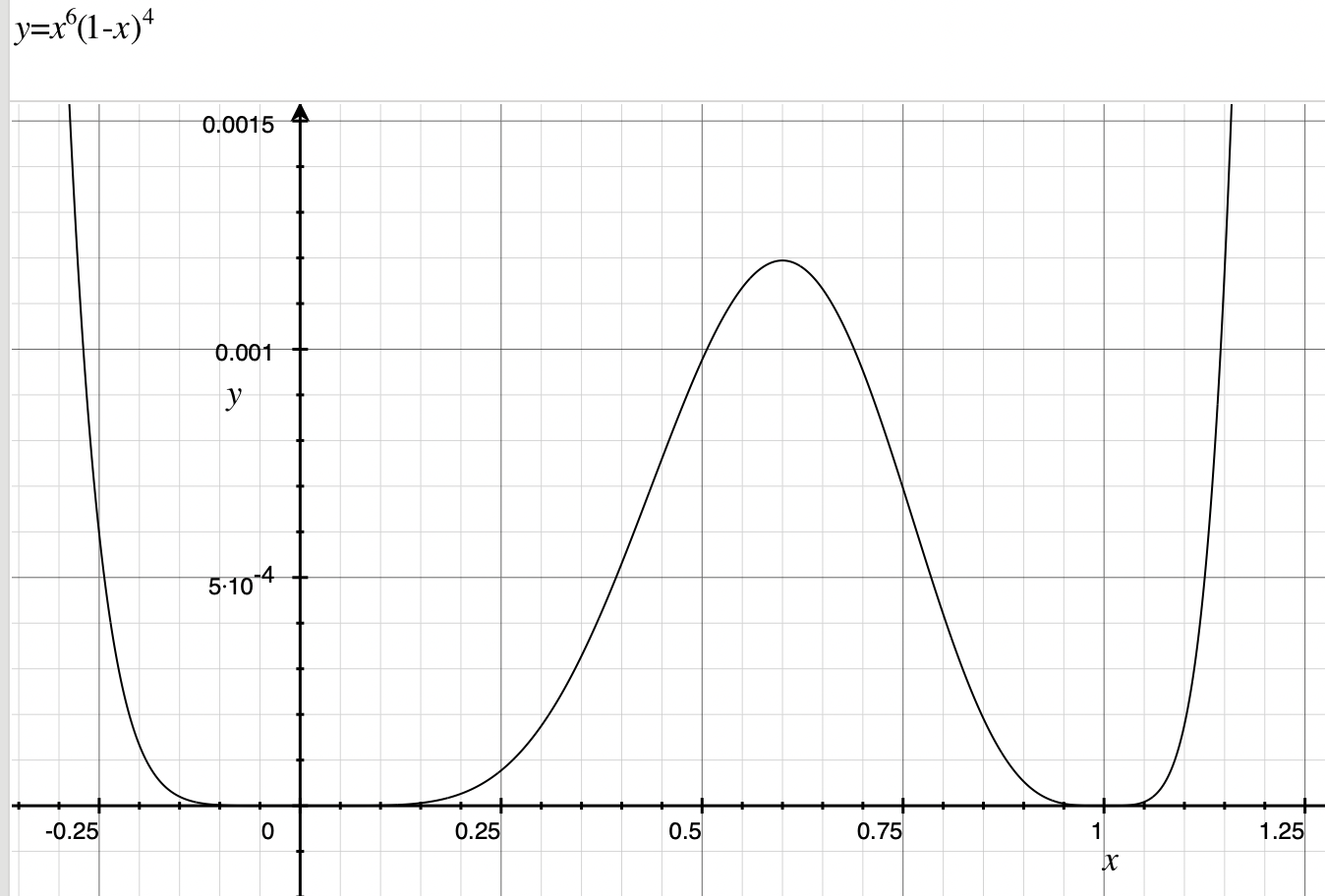
由于总体的似然就是每个样本似然的乘积,为了求解方便,通常会将似然函数转成对数似然函数,然后再求解。可以转成对数似然函数的主要原因是对数函数并不影响函数的凹凸性。
最大似然没有考虑先验知识,仅凭样本数据进行预估,在样本量小的时候容易产生过拟合。在上述的抛硬币case中,最大似然估计认为使似然函数 $P(X\mid\theta)$ 最大的参数 $θ$ 即为最好的 $θ$ ,此时最大似然估计是将 $θ$ 看作固定的值,只是其值未知。
最大后验概率估计
最大后验概率估计(Maximum A Posteriori Estimation)分布认为$θ$ 是一个随机变量,即$θ$ 具有某种概率分布,称为先验分布,求解时除了要考虑似然函数 $P(X\mid\theta)$ 之外,还要考虑$θ$ 的先验分布 $P(θ)$,因此其认为使 $P(X\mid\theta)P(\theta)$ 取最大值的$θ$ 就是最好的$θ$ 。此时要最大化的函数变为$P(X\mid\theta)P(\theta)$ ,由于$X$的先验分布$P(X)$是固定的(可通过分析数据获得,其实我们也不关心$X$的分布,我们关心的是$θ$ ),因此最大化函数可变为$\frac {P(X\mid\theta)P(\theta)}{P(X)}$ ,根据贝叶斯法则,要最大化的函数$\frac {P(X\mid\theta)P(\theta)}{P(X)} = P(\theta \mid X)$,因此要最大化的函数是 $P(\theta \mid X)$,而 $P(\theta\mid X)$是 $θ$ 的后验概率。最大后验概率估计可以看作是正则化的最大似然估计,当然机器学习或深度学习中的正则项通常是加法,而在最大后验概率估计中采用的是乘法, $P(\theta)$是正则项。在最大似然估计中,由于认为 $\theta$ 是固定的,因此 $P(\theta)=1$。
最大后验概率估计的公式表示: \(\underset{\theta}{\operatorname{argmax}} P(\theta \mid X) = \underset{\theta}{\operatorname{argmax}}\frac{P(X \mid \theta)P(\theta)}{P(X)}\) 因为给定样本 $x$ 后, $P(X)$ 在 $\theta$ 空间上为一个定值,和 $\theta$的大小没有关系,所以可以省略分母 $p(X)$。 可化简为: \(\underset{\theta}{\operatorname{argmax}} P(\theta \mid X) = \underset{\theta}{\operatorname{argmax}}{P(X \mid \theta)P(\theta)}\) 即为: \(\text { Posterior } \propto(\text { Likelihood } * \text { Prior })\) 在抛硬币的例子中,通常认为$θ=0.5$ 的可能性最大,因此我们用均值为$0.5$,方差为$0.1$的高斯分布来描述$θ$ 的先验分布,当然也可以使用其它的分布来描述 $θ$ 的先验分布。$θ$ 的先验分布为: \(P(\theta) = \frac{1}{\sqrt{2 \pi \sigma}} e^{-\frac{(\theta-\mu)^2}{2 \sigma^2}}=\frac{1}{10 \sqrt{2 \pi}} e^{-50(\theta-0.5)^2}\) 在最大似然估计中,已知似然函数为 $P(X\mid \theta)=\theta^6(1-\theta)^4$,因此要求$P(X \mid \theta)P(\theta)$的最大值,则 \(\operatorname {ln}^{'}(P(X \mid \theta)P(\theta))=0\) 得 \(100 \theta^3-150 \theta^2+40 \theta+6=0\) 由于 $0\leqslant \theta \leqslant 1$ ,解得 $\hat\theta =0.529$。
若使用$\alpha=3,β=3$ 的Beta分布来描述$θ$ 的先验分布,则 \(P(X \mid \theta) P(\theta)=\theta^6 \times(1-\theta)^4 \times \frac{1}{B(\alpha, \beta)} \times \theta^{\alpha-1}(1-\theta)^{\beta-1}\) 令$\operatorname {ln}^{‘}(P(X \mid \theta)P(\theta))=0$ 求解可得: \(\hat{\theta}=\frac{\alpha+5}{\alpha+\beta+8}=\frac{8}{3+3+8}=0.57\) 如果我们用均值为$0.6$,方差为$0.1$的高斯分布来描述$θ$ 的先验分布,则$\hat\theta =0.6$。由此可见,在最大后验概率估计中,$θ$ 的估计值与$θ $ 的先验分布有很大的关系。这也说明一个合理的先验概率假设是非常重要的。如果先验分布假设错误,则会导致估计的参数值偏离实际的参数值。
一般说来,先验分布 $p(θ)$ 是反映人们在抽样前对 $\theta$ 的认识,后验分布 $P(θ\mid X)$ 是反映人们在抽样后对 $\theta$ 的认识,之间的差异是由于样本的出现后人们对$\theta$ 认识的一种调整,所以后验分布 $P(θ\mid X)$ 可以看作是人们用总体信息和样本信息(抽样信息)对先验分布 $P(θ)$ 作调整的结果。而当我们对 $\theta$ 有百分百的自信时,再多数据都无法更新参数的后验分布。
共轭分布
在贝叶斯统计中,如果后验分布与先验分布属于同类,则先验分布与后验分布被称为共轭分布,而先验分布被称为似然函数的共轭先验。
二项分布参数的共轭先验是Beta分布,多项式分布参数的共轭先验是Dirichlet分布,指数分布参数的共轭先验是Gamma分布,⾼斯分布均值的共轭先验是另⼀个⾼斯分布,泊松分布的共轭先验是Gamma分布。
意义:因为后验分布和先验分布形式相近,只是参数有所不同,这意味着当我们获得新的观察数据时,我们就能直接通过参数更新,获得新的后验分布,此后验分布将会在下次新数据到来的时候成为新的先验分布。如此一来,我们更新后验分布就不需要通过大量的计算,十分方便。
贝叶斯估计
贝叶斯估计,假定把待估计的参数看成是符合某种先验概率分布的随机变量,而不是确定数值。在样本分布上,计算参数所有可能的情况,并通过计算参数的期望,得到后验概率密度。
贝叶斯估计是最大后验估计的进一步扩展,贝叶斯估计同样假定$θ$ 是一个随机变量,但贝叶斯估计并不是直接估计出$θ$ 的某个特定值,而是估计$θ$ 的分布,这是贝叶斯估计与最大后验概率估计不同的地方。在贝叶斯估计中,先验分布$P(X)$ 是不可忽略的(因为不是像MAP那样求最大值,所以即使$P(X)$ 是常数也不能忽略)。回到抛硬币的例子中,在已知$X$ 的情况下,描述$θ$ 的分布即描述$P(θ \mid X)$,$P(θ \mid X)$是一种后验分布。如果后验分布的范围较窄,则估计值的准确度相对较高,反之,如果后验分布的范围较广,则估计值的准确度就较低。
贝叶斯公式: \(P(\theta \mid X)=\frac{P(X \mid \theta) P(\theta)}{P(X)}\) 在连续型随机变量中,由于$P(X) = \int_{\Theta} P(X \mid \theta) P(\theta) d \theta$ ,因此贝叶斯公式变为: \(P(\theta \mid X)=\frac{P(X \mid \theta) P(\theta)}{\int_{\Theta} P(X \mid \theta) P(\theta) d \theta}\) 从上面的公式中可以看出,贝叶斯估计的求解非常复杂,因此选择合适的先验分布就非常重要。一般来说,计算积分$\int_{\Theta} P(X \mid \theta) P(\theta) d \theta$是不可能的。对于这个抛硬币的例子来说,如果使用共轭先验分布,就可以更好的解决这个问题。二项分布参数的共轭先验是Beta分布,由于$θ$ 的似然函数服从二项分布,因此在贝叶斯估计中,假设$θ$ 的先验分布服从$P(\theta) \sim \operatorname{Beta}(\alpha, \beta)$,Beta分布的概率密度公式为: \(f(x ; \alpha, \beta)=\frac{1}{B(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1}\) 因此,贝叶斯公式可以写作: \(\begin{aligned} P(\theta \mid X) & =\frac{P(X \mid \theta) P(\theta)}{\int_{\Theta} P(X \mid \theta) P(\theta) d \theta} \\ & =\frac{\theta^6(1-\theta)^4 \frac{\theta^{\alpha-(1-\theta)^{\beta-1}}}{B(\alpha, \beta)}}{\int_{\Theta} \theta^6(1-\theta)^4 \frac{\theta^{\alpha-(1-\theta)^{\beta-1}}}{B(\alpha, \beta)} d \theta} \\ & =\frac{\theta^{\alpha+6-1}(1-\theta)^{\beta+4-1}}{\int_{\Theta} \theta^{\alpha+6-1}(1-\theta)^{\beta+4-1} d \theta} \\ & =\frac{\theta^{\alpha+6-1}(1-\theta)^{\beta+4-1}}{\operatorname{B}(\alpha+6-1, \beta+4-1)} \\ & =\operatorname{Beta}(\theta \mid \alpha+6-1, \beta+4-1) \\ & =\operatorname{Beta}(\theta \mid \alpha+6, \beta+4) \end{aligned}\) 从上面的公式可以看出,$P(\theta) \sim \operatorname{Beta}(\theta \mid \alpha+6, \beta+4)$。其中B函数,也称Beta函数,是一个标准化常量,用来使整个概率的积分为1。$\operatorname{Beta}(\theta \mid \alpha+6, \beta+4)$ 就是贝叶斯估计的结果。
如果使用贝叶斯估计得到的$θ$分布存在一个有限均值,则可以用后验分布的期望作为$θ$的估计值。假设$\alpha=3,β=3$,根据Beta分布的数学期望公式可得: \(\hat{\theta}=\int_{\Theta} \theta P(\theta \mid X) d \theta=E(\theta)=\frac{\alpha}{\alpha+\beta}=\frac{9}{9+7}=0.5625\)
总结
从最大似然估计、最大后验概率估计到贝叶斯估计,从下表可以看出$θ$ 的估计值$\hat \theta$ 是逐渐接近0.5的。从公式的变化可以看出,使用的信息是逐渐增多的。最大似然估计、最大后验概率估计中都是假设$θ$ 未知,但是确定的值,都将使函数取得最大值的$θ$ 作为估计值,区别在于最大化的函数不同,最大后验概率估计使用了$θ$ 的先验概率。而在贝叶斯估计中,假设参数$θ $ 是未知的随机变量,不是确定值,求解的是参数$θ$ 在样本$X$ 上的后验分布。
| Type | MLE | MAP | BE |
|---|---|---|---|
| $\hat\theta$ | 0.6 | 0.57 | 0.5625 |
| f | $P(X \mid \theta)$ | $P(X \mid \theta)P(\theta)$ | $\frac{P(X \mid \theta)}{P(X)}$ |
- MLE 求解步骤
- 确定似然函数
- 将似然函数转换为对数似然函数
- 求对数似然函数的最大值(求导,解似然方程)
- MAP 求解步骤
- 确定参数的先验分布以及似然函数
- 确定参数的后验分布函数
- 求后验分布的对数函数的最大值(求导,解方程)
- BE 求解步骤
- 确定参数的似然函数
- 确定参数的先验分布,应是后验分布的共轭先验
- 确定参数的后验分布函数
- 根据贝叶斯公式求解参数的后验分布
