背景
Stable Diffusion是一种扩散模型(diffusion model)的变体,叫做“潜在扩散模型”(latent diffusion model; LDM)。扩散模型是在2015年推出的,其目的是消除对训练图像的连续应用高斯噪声,可以将其视为一系列去噪自编码器。Stable Diffusion由3个部分组成:变分自编码器(VAE)、U-Net和一个文本编码器。
VAE
变分自编码器(Variational Autoencoder,VAE)是由Diederik P. Kingma和Max Welling提出的一种人工神经结构,属于概率图模式和变分贝叶斯方法。
VAE与自编码器模型有关,因为两者在结构上有一定亲和力,但在目标和数学表述上有很大区别。VAE属于概率生成模型(Probabilistic Generative Model),神经网络仅是其中的一个组件,依照功能的不同又可分为编码器和解码器。编码器可将输入变量映射到与变分分布的参数相对应的潜空间(Latent Space),这样便可以产生多个遵循同一分布的不同样本。解码器的功能基本相反,是从潜空间映射回输入空间,以生成数据点。虽然噪声模型的方差可以单独学习而来,但它们通常都是用重参数化技巧(Reparameterization Trick)来训练的。
此类模型最初是为无监督学习设计的,但在半监督学习和监督学习中也表现出卓越的有效性。
VAE的结构与操作概述
VAE是一个分别具有先验和噪声分布的生成模型,一般用最大期望算法(Expectation-Maximization meta-algorithm)来训练。这样可以优化数据似然的下限,用其它方法很难实现这点,且需要 $q$ 分布或变分后验。这些 $ q$ 分布通常在一个单独的优化过程中为每个单独数据点设定参数;而VAE则用神经网络作为一种摊销手段来联合优化各个数据点,将数据点本身作为输入,输出变分分布的参数。从一个已知的输入空间映射到低维潜空间,这是一种编码过程,因此这张神经网络也叫“编码器”。
解码器则从潜空间映射回输入空间,如作为噪声分布的平均值。也可以用另一个映射到方差的神经网络,为简单起见一般都省略掉了。这时,方差可以用梯度下降法进行优化。
优化模型常用的两个术语是“重构误差(reconstruction error)”和“KL散度”。它们都来自概率模型的自由能表达式(Free Energy Expression ),因而根据噪声分布和数据的假定先验而有所不同。例如,像IMAGENET这样的标准VAE任务一般都假设具有高斯分布噪声,但二值化的MNIST这样的任务则需要伯努利噪声。自由能表达式中的KL散度使得与 $p$ 分布重叠的 $q$ 分布的概率质量最大化,但这样可能导致出现搜寻模态(Mode-Seeking Behaviour)。自由能表达式的剩余部分是“重构”项,需要用采样逼近来计算其期望。
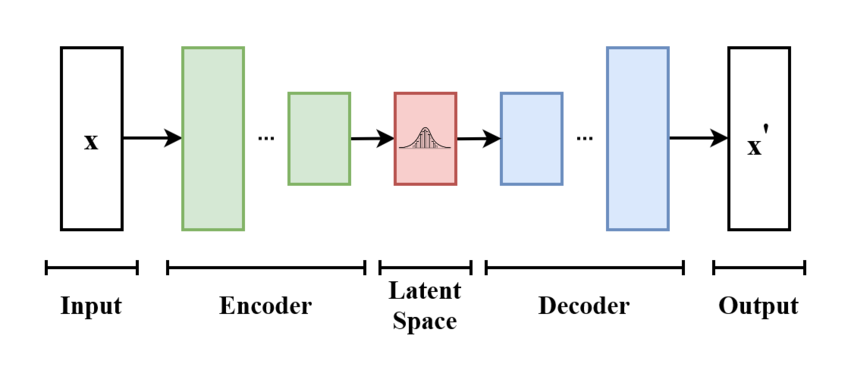
VAE的基本框架。模型接受 $x$ 为输入。编码器将其压缩到潜空间。解码器以在潜空间采样的信息为输入,并产生 $x’$ ,使其与 $x$ 尽可能相似。
| 从建立概率模型的角度来看,人们希望用他们选择的参数化概率分布 $p_\theta(x) = p(x|\theta)$ 使数据 $x$ 的概率最大化。这一分布常是高斯分布 $N(x | \mu, \sigma)$ ,分别参数化为 $\mu$ 和 $\sigma$ ,作为指数族的一员很容易作为噪声分布来处理。简单的分布很容易最大化,但如果假设了潜质(latent)$z$ 的先验分布,可能会产生难以解决的积分。 |
逆变换采样 (inverse transform sampling)
严格单调递增的累积分布函数服从均匀分布。
\[\begin{align} &令Y= F(X),则有0 \leq Y \leq 1\\ &P(Y \leq y)=P(F(x) \leq y)=P(X \leq F^{-1}(y))=F(F^{-1}(y))=y\\ &所以Y~U(0,1) \end{align}\]
re-parameterization
Gumbel 分布
